
I have attempted speedblind on 3x3x3 one time, and I missed by 3 pieces. I could probably do the speedblind thing, but I always figured there was a better way. Wouldn't it be nice to memorize how to get the pieces to square in advance, so you would be able to skip the speedblind step? It always seemed to me that it should be possible, but I never quite did the work to make sure it was.
For some time, Jim Mertens has been telling me I should try taking a break from big cube BLD to see if I might improve from the break. After US Nationals 2010, I decided I would finally try that. But of course, I couldn't take a break from all things BLD, so I figured I would instead work on my dream method for solving square-1 BLD. I was very pleasantly surprised in that it only took me about a week to work out my first translation matrix, and be able to solve one of the 90 possible shapes consistently in less than 10 minutes. So I spent the next couple of weeks working out the other cases, and here we are!
I should probably mention that there is really nothing particularly revolutionary about this method. Other than a speedblind method like I mentioned earlier, this really is the obvious way to go about doing this. I guess I was just the first person crazy enough to be willing to spend the time memorizing all the cases. What little innovation I've done here is to provide some mechanisms for handling the lettering so that the memorization is practical, but I'm sure anyone could have done that with a little thought.
Second, I hope people will not be scared off by the size of this tutorial. It's very difficult to talk about the square-1 because of its shape-changing ability, so some of the descriptions here take many words to describe a simple concept. I recommend that you simply skim the material in these instructions down to the Sample Solve, then go to the Sample Solve and try to work through it until you understand how it works, referring to the other sections as needed when you encounter something you don't understand. Then, if you're still interested, try a solve with "open notes". Apply a scramble, use the Memorization List to find your case, and try memorizing with the translation matrix in front of you. If you can, then you know that you know how to solve square-1 BLD with my method - all you lack is memorizing the 90 cases. Then, if you get really ambitious, you can consider actually committing the 90 cases to memory so you can truly say you know how to do square-1 BLD. But I think it can still be fun if you have to look at the table, even if it isn't a full legitimate BLD solve.
Third, I generated all of this manually. For the Memorization List, I actually wrote all cases on paper, and then typed them in here. So it is very possible that I have made mistakes. If so, please contact me and I will try to correct the mistakes.
Fourth, if you really decide you would like to learn the full method, I recommend that you use an advanced memory technique for memorizing the Memorization List. I memorize the letters in pairs, where each pair of letters is represented by an image. Since the letters range from A to W, that means I have 576 images prepared for all the possible 2-letter combinations. Then I put the images together into a "story". I pair the shape name and the helper, then create 2 sub-stories that go with that pair, one for the edges, and the other for the corners. For instance, for the first case in my table, TW, I remember the following:
I use a "helper" image to help me remember where to start lettering the pieces, so I can reliably know how to use the matrix. The helper also is beneficial in that it helps me get to square - I'm still not good at getting to square optimally, but the helper guarantees that I will get there not only optimally but consistently. If you don't make the same moves to get to square every time, you won't know where the pieces are once you get there. The helper (along with some rules for rotationally symmetric cases) guarantees that you will always use the same moves to get to square. (Eventually, an expert might not need it for that, but it's helpful until someone gets that good, anyway.)
Solving is very much like solving a 3x3x3 BLD. Well, first you have to get to square, but after that, it's pretty much the same. The nice thing is that you don't have to worry about orientation on a square-1 - just permutation. So get each of the 16 pieces to the proper place and you're done. I use 3 cycles of edges and corners, and 2 cycles for parity cases, with J perms if there is a 2 cycle of both corners and edges. Solving is obviously the easy part.
| Side | Edges | Corners |
|---|---|---|
| * A * | I * J | |
| Top | D * B | * * * |
| * C * | L * K | |
| ________ | ________ | ________ |
| * E * | M * N | |
| Bottom | H * F | * * * |
| * G * | P * O | |
These are the letters I actually memorize for a given solve.
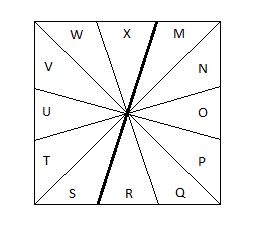
I use a translation matrix to generate the memorization. For that matrix, I label each 30 degree slice with a letter, starting at the first piece clockwise of the slice (at about 1 o'clock) as A, going all the way around to L, and then on the bottom starting at M and working my way around to X. What this means is that any edge piece, since it is 30 degrees, will cover just one letter, and a corner piece, since it is 60 degrees, will cover two letters. For corner pieces, I assign the first of the two letters as the name of the location of that piece.


Now, I can create a translation matrix for a given shape as follows (this is how I built the Memorization List below):
When finished, the results A to H are the translation matrix for edges, and the results for I to P are the translation matrix for corners. Using this matrix, for a given scramble of that shape, I can ask "What piece will be at position z in the cube once I solve to square", go to that item in the translation matrix, and know where that piece is in the scrambled puzzle. This is all I need to then be able to memorize it as if it were already square. That may not be intuitive to see from this description, but I'm hoping the Sample Solve will make it clearer.
| Name | Bit Pattern | Common Name |
|---|---|---|
| (None) | 111111 | star |
| ______ | __________ | ____________________ |
| 0 | 1100000000 | - |
| 1 | 1010000000 | - |
| 2 | 1001000000 | - |
| 3 | 1000100000 | - |
| 4 | 1000010000 | - |
| ______ | __________ | ____________________ |
| A | 1111100 | paired edges |
| B | 1111010 | perpendicular edges |
| C | 1110110 | parallel edges |
| ______ | __________ | ____________________ |
| D | 111000000 | 6 |
| E | 110100000 | right 5-1 |
| F | 110010000 | right 4-2 |
| G | 110001000 | 3-3 |
| H | 110000100 | left 4-2 |
| I | 110000010 | left 5-1 |
| J | 101010000 | 4-1-1 |
| K | 101001000 | 3-1-2 |
| L | 101000100 | 3-2-1 |
| M | 100100100 | 2-2-2 |
| ______ | __________ | ____________________ |
| N | 11110000 | scallop |
| O | 11101000 | right pawn |
| P | 11100100 | shield |
| Q | 11100010 | left pawn |
| R | 11011000 | mushroom |
| S | 11010100 | left fist |
| T | 11010010 | kite |
| U | 11001100 | barrel |
| V | 11001010 | right fist |
| W | 10101010 | square |
When I start to memorize, after figuring out what shape I have, I put one finger on the "A" piece on the top side, and another finger on the "A" piece of the bottom side. I then know those pieces are A (for the top side A-L when interpreting the matrix) and M (for the bottom side M-X when interpreting the matrix) when finding the next piece to memorize.
We'll use the following random scramble (generated from qqtimer):
The first thing I would do when starting memorization is to determine the shape. This one is KB. It's nice because the K is on top and the B is on bottom. Sometimes the sides are reversed, so that the one that is normally on top is on the bottom. When this happens, you have to do a bit of extra work. You memorize treating the top side as the bottom and the bottom as the top. Then when you start to solve, you first perform /(6,6)/(6,6), which puts things the way you're used to, and you proceed from there. That guarantees that you solve to square consistently, with every piece where you expect it to be.
Now I would use my shape name KB to recall my helper, which for KB is IB. To determine the lettering scheme, I start with the counterclockwise-most corner piece that's closest to another corner piece, which after scrambling is the corner piece that is at ULB. I treat it as "A", and increase the letter for every piece as I count around, arriving at "I" (the first letter in my helper) at the edge piece just to the left of the "A" piece. I will count this location (which you can see is at UL) as the letter A in my translation matrix, and then work around the top clockwise, assigning a new letter to each 30 degree slice. So the pieces on top will be labeled A, B, D, E, G, H, I, K, L. (If you follow what I mean, you'll see that the skipped letters correspond to the corners, since they take up 2 30 degree slices.) For the bottom (looking at it by tilting the puzzle so I'm looking directly at the bottom of the puzzle), again I start with the counterclockwise-most corner piece that's closest to another corner piece, which in this case is the corner at DBR. I treat it as "A", and increase the letter as I count around clockwise, arriving at "B", the very next corner clockwise of that first one. I count that location (which you can see is at DBL) as the letter M in my translation matrix, and work around the bottom clockwise, assigning a new letter to each 30 degree slice. So the pieces on bottom will be labeled M, O, Q, S, T, V, W, starting with that M piece.
Now I know how to apply my translation matrix, so I can begin calculating my cycles. I solve edges first, then corners. I always start with edge piece "A" in the squared puzzle (I will always call the resulting puzzle after returning it to square the "squared puzzle", for short), as the start of my first cycle. So I will not memorize A (it is my buffer piece), but first I must memorize the piece that will be at location "A" once I have the squared puzzle. Note that my translation matrix for edges for this case (KB) is GD KA HL SV. The first letter in this matrix means that the piece that will be at "A" in the squared puzzle is now at "G" (counting as I described above for the top layer). If you look at the scrambled puzzle, you will see that, counting from the "A" piece (which I know is at UL from my helper, as described above), the "G" piece is at UR. The piece which is there is the piece which belongs at DB (which I label as "G"). So my first piece to memorize for solving the puzzle is "G".
Now I need to find the piece that will be at G in the squared puzzle, to find the next piece to memorize. That will be the 7th letter in my translation matrix (since G is the 7th letter of the alphabet), which is "S". So I must go to my scrambled puzzle and find the position "S" to see what is there. Starting at DBL, I count to the letter S, which is at DF. The piece which is there is the piece which belongs at DR (which I label "F"), so my second letter to memorize for solving the puzzle is "F". My memorization so far is GF.
I now continue this process the same until I finish the cycle:
So I know that once I have the squared puzzle, my memorization will be GF EH CB D, meaning that piece A (my buffer) needs to go to G, piece G needs to go to F, piece F needs to go to E, piece E needs to go to H, piece H needs to go to C, piece C needs to go to B, piece B needs to go to D, and piece D needs to go to my buffer location A. I'm finished memorizing edges. I always memorize in image pairs, so I quickly see here that I have a single letter left over. That means I'll have edge parity when I finish solving the edges. I always make sure my edge parity is at A and D, so I won't have to remember it, and so I put my feet together at this point to indicate that I have edge parity. That way I'll never DNF because I forgot to do parity.
Now to memorize the corners. It works the same, but this time working with the second matrix for case KB, the corner matrix, which is QB EO WI MT. This says that my buffer corner piece in the squared puzzle (which I call "I") will be at location Q in the scrambled puzzle (since I is the first corner letter, and Q is the first letter in my corner matrix). Counting from the "M" piece, which is at DBBL, we see that the "Q" piece is DFL in the scrambled puzzle. The piece there belongs at "K" in the squared puzzle, so my first letter to memorize is "K", since it is the piece that will be at the buffer location in the squared puzzle.
Now I want to find the piece that will be at "K" in the squared puzzle, and since K is the third corner letter, I look at the third letter in my matrix, which is "E". The piece at "E" (which is UBR) belongs at "O" in the squared puzzle, so my second letter to memorize is "O". I add "O" to my memorization, giving me KO.
I now continue this process similarly until I finish the cycle:
Final memorization:
Now it's time to solve. I put on the blindfold and begin getting to square. My helper (IB) tells me I need to move the piece at UL to the position to the right of the back slice on top, and I need to move the piece that's currently at DBBL to the position to the right of the front slice on the bottom. I do those moves (which is (4,6), but I don't usually think about that), and then do the slice move. I then feel the resulting shape and discover that the top is P and the bottom is W - the shape is PW (which is shield-square). My helper for case PW is CB, so I can use that to figure out how I need to move the pieces for the next slice. On top, the third piece (because C is the third letter, from my helper CB) counting from the counterclockwise-most of the adjacent corner pieces is at UFFR, so I need to turn that piece so it is to the right of the back slice on top. For the bottom, I need an edge piece, since the corner counts as A for the square case and the edge counts as B. My rule for square shapes (see rules below in the memorization list section) indicates I want to move it as little as possible, and I can see that it is already in an acceptable position, so I don't need to move the bottom. So now (after (-4,0), which takes care of the P piece) I do another slice move and I see I am at fist-fist. From this point, I just know how to solve fist-fist - I always do minimum moves to align the next pieces - in this case, I apply (-1,0)/(-3,0)/, and I'm done. The puzzle is square.
If you're following along, it might be worth it to look at the puzzle now and confirm for yourself that our memorization was correct. Starting with the buffer edge piece UB, you should see that our cycle is indeed GFEHCBD, and starting with the buffer corner piece UBL, you should see that the corner cycle is indeed KOMJN. So now we just have the relatively easy task of solving these pieces.
I use 3 cycles for everything (except the last 2 pieces, if there's parity). So our first cycle will be A->G->F. To do this, I setup to a counterclockwise U perm by doing (-2,-3)/(-1,0). Then I perform the counterclockwise U perm (1,0)/(0,-3)/(-1,0)/(3,0)/(1,0)/(0,3)/(-1,0)/(-3,0)/, and then undo the setup with (1,0)/(2,3). Now the pieces at "G" and "F" are solved.
Next, I solve the next two pieces EH by doing A->E->H. Again I set up to the counterclockwise U perm, this time by doing (-2,3)/(-1,0). Then I perform the same counterclockwise U perm (1,0)/(0,-3)/(-1,0)/(3,0)/(1,0)/(0,3)/(-1,0)/(-3,0)/, and then undo the setup with (1,0)/(2,-3). Now the pieces at "E" and "H" are also solved.
Next, I solve the next two pieces CB by doing A->C->B. This one also requires the counterclockwise U perm (this probably wasn't such a good example, was it?), so I set up with (-3,0). Then I do the same algorithm (1,0)/(0,-3)/(-1,0)/(3,0)/(1,0)/(0,3)/(-1,0)/(-3,0)/, and undo the setup with (3,0). Now all the edges are solved except A and D.
I consider this "edge parity", because I have 2 edges unsolved. I like to keep the parity edges at A and D for solving later, since I use the I piece as my corner buffer, which means it is easy to do a J perm to fix if the corners also have parity. This particular solve also has "corner parity", so it will be good for using a J perm to fix at the end. If it did not, I might consider doing the adjacent edge parity fix at this point in the solve.
Now for the corners. First up is the pair KO, so I want to solve I->K->O. This is a bad one to set up, requiring two moves. I set it up to a clockwise A perm with (1,3)/(0,-3)/(2,0). Then I do the A perm (1,0)/(0,3)/(2,0)/(-3,0)/(-2,0)/(0,-3)/(2,0)/(3,0)/(-3,0), and then undo the setup with (-2,0)/(0,3)/(-1,-3). Now the pieces at "K" and "O" are solved.
Next, I solve the two pieces MJ by doing I->M->J. This one is easier to set up: (-2,3)/(-4,0), which sets up for a counterclockwise A perm, /(-3,0)/(-2,0)/(0,3)/(2,0)/(3,0)/(-2,0)/(0,-3)/(2,0). Then I undo the setup moves with (4,0)/(2,-3), and the pieces at "M" and "J" are solved.
Now all that's left are the last 2 edges and the last 2 corners. Setup moves (0,-1)/(0,1) prepare for the J perm (-2,0)/(0,-3)/(0,3)/(0,-3)/(3,0)/(-3,3)/(5,0). Now just undo the setup moves with (0,-1)/(0,1), and it's solved! Well, except for the fact that the middle slice is wrong, so just do /(6,0)/(6,0)/(6,0), and now it's REALLY solved!
edges:
Edges: GD BA HE FC
I won't go into how I got these, but if you simply use the translation matrix looking for what piece is at each location (A-H for edges, and I-P for corners), you should wind up with these. Then, when solving, you know where all the pieces are, and you work out the cycles from there. So if you start with A (which is G in our memorization), you then see what's at G (F, since it's the 7th letter), and therefore figure the first cycle is A->G->F, and solve that. Then you go onto the piece that's at F (E) and the piece that's at E (H), and so you solve A->E->H, and so on. You'll find that you still wind up doing the same solve, you just do the memorization a little differently.
I've tried this method, and it also works pretty well. The memorization phase is much quicker, since you have less to keep track of. But unfortunately, working out the cycles during the solve is a little more difficult than it is pre-solve, because it's harder to keep track of what has already been solved. I suspect that if you don't need to break into new cycles, this method might work out best. But it seems like the method I normally use is a little better if you do have to break into new cycles.
This list contains each of the 90 possible cases. For each case, I have provided the following:
Sample Solve
It often seems that the best possible way to understand a BLD method is to see a sample solve, with explanations as to the thought processes required to carry out that solve. So I will focus on that here.
(-3,-3) / (-3,0) / (-3,5) / (-5,4) / (-3,-4) / (0,-3) / (-1,-3) / (2,6) / (0,1) / (6,1) / (-2,4) / (0,2) / (0,2) / (2,4) / (-5,2) /
Edges: GFEHCBD
Corners: KOMJN
Algorithms
I use the following algorithms for solving square-1 BLD. There are several others I should probably learn, but these are the ones I know now; they're fairly reliable, and they require at most one setup slice move for edges and 2 setup slice moves for corners. I will use my lettering scheme to describe the letters that are being solved, since it's easier than giving the locations with UDRLFB.
corners:
parity:
Alternate Approach
Joey Gouly has suggested an alternate approach for this method. His suggestion is that you merely memorize where all the pieces will be at the beginning, and then work out the cycles while in the solving phase. So for instance, in the Sample Solve above, you would memorize the following, telling what piece is at each location:
Corners: KN OL JI MP
Memorization List
Note that this list and the diagrams were originally created by Christian Eggermont. I'd like to thank him very much for allowing me to use his page as a starting point for this one, and also for creating the list in the first place - it was very useful in the creation of this method.
Note: I made one big mistake when doing one of the cases. If you line up the case for EA with the helper DE, it goes to the upside-down version of NT. (So, it's TN instead of NT.) I'm afraid that the easiest thing I can suggest to you is that you use the "Moves to get to square" to memorize this case. There are too many cases that pass through EA to get to square, so I'm not going to go through and fix them all, especially since I want this to reflect my method for solving. I am sorry about that.
It takes a while to do it this way - I've sometimes taken several minutes when I have trouble remembering one of the helpers - but it's almost guaranteed to work. The one place where I know it doesn't work (there might be more - I've tried not to make them) is for the case TU; I did that case before I realized I should follow this rule. If you decide to generate your own table (rather than using mine), please remember that it is very nice to have all the shapes follow the same path, where possible.
One thing that does make this difficult is that there are some cases where there are multiple possible ways to align the pieces for the next turn, due to rotational symmetry. To help with that, I use the following rules, which work for the solutions I give below:
| Shape | Case | Helper | Edges | Corners | Distance | Moves to get to square | Moves to get to this shape | Probability |
|---|---|---|---|---|---|---|---|---|


|
TW | HA (leads to SS) | OI XR FA UJ | PG BM DS KV | 7 | (0,0)(3,1)(-2,-1)(-4,6)(0,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(0,2)(4,6)(2,1)(-3,-1) | 16 / 3678 |


|
1 | JA (leads to DB) | LD JH IA KG | EB MU OW QS | 6 | (0,0)(-2,2)(-3,-2)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(3,2)(2,-2) | 16 / 3678 |


| 3 | BA (leads to NQ) | FH BJ AG CI | KU OM SQ WD | 6 | (0,0)(4,0)(1,2)(3,-2)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,2)(-1,-2)(-4,0) | 16 / 3678 |


| MB | AE (leads to KA) | LG CP MD HK | NQ UW AS EI | 6 | (0,0)(-1,-2)(-4,4)(-2,6)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,6)(4,-4)(1,2) | 16 / 3678 |


| MC | AD (leads to GA) | DK MG LH CR | UI EA NS PW | 6 | (0,0)(-1,-2)(5,-2)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(-5,2)(1,2) | 8 / 3678 |


| RV | CA (leads to NS) | HU RA QF GX | BS IM OD VK | 6 | (0,0)(2,-3)(-3,6)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(3,6)(-2,3) | 48 / 3678 |


| RT | CB (leads to OV) | FR GO SH VA | MP ID KT BW | 6 | (0,0)(4,-1)(-4,6)(0,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(0,2)(4,6)(-4,1) | 32 / 3678 |


| RU | HC (leads to NR) | AK MT LF NS | UI BO QD GW | 6 | (0,0)(-2,0)(6,-4)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(6,4)(2,0) | 32 / 3678 |


| RS | HG (leads to NV) | NA LS KV MF | QW OI BT DG | 6 | (0,0)(-4,5)(-3,4)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(3,-4)(4,-5) | 48 / 3678 |


| TV | BA (leads to QW) | FC RJ QG UX | OA DK MS HV | 6 | (0,0)(2,0)(1,0)(-2,0)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,0)(-1,0)(-2,0) | 48 / 3678 |


| UV | CA (leads to NO) | HX BR AU GQ | CV IS MK OE | 6 | (0,0)(0,4)(-1,-2)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(1,2)(0,-4) | 48 / 3678 |


| SS | HG (leads to OV) | FL MI SN VA | GJ OD QT BW | 6 | (0,0)(-2,-1)(-4,6)(0,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(0,2)(4,6)(2,1) | 36 / 3678 |


| SW | CA (leads to OT) | XR HU AG DO | MP IS VB EK | 6 | (0,0)(4,-3)(5,4)(0,2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,-2)(-5,-4)(-4,3) | 24 / 3678 |


| TS | FG (leads to OW) | LI ND MA SV | QE JW OG BT | 6 | (0,0)(-2,0)(-3,2)(-2,0)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,0)(3,-2)(2,0) | 48 / 3678 |


| US | AG (leads to NQ) | VL FN EK SM | OA GQ WI CT | 6 | (0,0)(0,-4)(1,2)(3,-2)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,2)(-1,-2)(0,4) | 48 / 3678 |


| UW | CA (leads to OO) | BR HX OG UA | CS IM EP KV | 6 | (0,0)(4,4)(3,0)(4,4)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(-4,-4)(-3,0)(-4,-4) | 16 / 3678 |


| WV | BE (leads to TQ) | DO XR JW AG | HS MP EK UB | 6 | (0,0)(3,-4)(2,1)(0,-2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,2)(-2,-1)(-3,4) | 24 / 3678 |


| VV | HA (leads to QS) | QJ XG RA FU | MH VD KO BS | 6 | (0,0)(2,1)(6,-4)(0,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(0,2)(6,4)(-2,-1) | 36 / 3678 |


| DB | BD (leads to EA) | JR HF GO IE | SP KW AM CU | 5 | (0,0)(-3,-2)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(3,2) | 48 / 3678 |


| DC | AD (leads to 0) | HJ LR IK MG | SW CP UA EN | 5 | (0,0)(3,0)(2,4)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(-2,-4)(-3,0) | 24 / 3678 |


| EC | HD (leads to FA) | AJ LR BK MG | UH EP WC NS | 5 | (0,0)(5,0)(0,2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,-2)(-5,0) | 24 / 3678 |


| FB | BD (leads to EA) | JR HD GO IC | EP KU WM AS | 5 | (0,0)(-3,0)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(3,0) | 64 / 3678 |


| GA | AF (leads to EA) | NJ LF KG ME | SH OW AQ CU | 5 | (0,0)(5,-2)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(-5,2) | 72 / 3678 |


| GC | AD (leads to FA) | EJ LR FK MG | AH UP CS NW | 5 | (0,0)(5,-4)(0,2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,-2)(-5,4) | 24 / 3678 |

| HB | HD (leads to EA) | JR HB GO IA | CP KS UM WE | 5 | (0,0)(-3,2)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(3,-2) | 64 / 3678 |


| IC | GD (leads to EB) | JD LA KM RI | WB ES UP NG | 5 | (0,0)(-3,6)(-2,6)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,6)(3,6) | 24 / 3678 |


| JC | AD (leads to EB) | JF LC KM RI | AD SU WP NG | 5 | (0,0)(-3,4)(-2,6)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,6)(3,-4) | 32 / 3678 |


| KA | AF (leads to EB) | KF MC LN GJ | AD SU WQ OH | 5 | (0,0)(-4,4)(-2,6)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,6)(4,-4) | 72 / 3678 |


| KC | ID (leads to GB) | RK LH GM AD | UI EP SW NB | 5 | (0,0)(-5,2)(0,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(0,2)(5,-2) | 24 / 3678 |


| LA | GF (leads to EA) | NJ LD KG MC | EH OU WQ AS | 5 | (0,0)(5,0)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(-5,0) | 72 / 3678 |


| LC | GD (leads to FA) | CJ LR DK MG | WH SP AE NU | 5 | (0,0)(5,-2)(0,2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,-2)(-5,2) | 24 / 3678 |


| NQ | GD (leads to IA) | RL NB MK OA | CU GE SI WP | 5 | (0,0)(1,2)(3,-2)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,2)(-1,-2) | 48 / 3678 |


| NP | BD (leads to 2) | HM RJ IG NQ | WK SC UE AO | 5 | (0,0)(5,0)(-4,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(4,2)(-5,0) | 72 / 3678 |


| NO | CD (leads to EA) | HP RF QM GE | SN IW AK CU | 5 | (0,0)(-1,-2)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(1,2) | 48 / 3678 |


| NR | AC (leads to EA) | MI KT JR LS | UG NA CP EW | 5 | (0,0)(6,-4)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(6,4) | 48 / 3678 |


| NV | BE (leads to EA) | JR HX GO IW | AP KE SM UC | 5 | (0,0)(-3,4)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(3,-4) | 72 / 3678 |


| NS | BB (leads to EA) | JR HV GO IU | WP KC EM SA | 5 | (0,0)(-3,6)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(3,6) | 72 / 3678 |


| NW | BA (leads to EB) | GX IU HJ OR | SV AC EM KP | 5 | (0,0)(0,-2)(-2,6)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,6)(0,2) | 24 / 3678 |


| OP | AG (leads to EA) | NJ LV KG MU | WH OC EQ SA | 5 | (0,0)(5,6)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(-5,6) | 48 / 3678 |


| OO | AD (leads to 4) | RJ LP GK MQ | SW AE UH CN | 5 | (0,0)(3,0)(4,4)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(-4,-4)(-3,0) | 16 / 3678 |


| OR | AC (leads to FA) | SJ LR TK MG | CH WP EU NA | 5 | (0,0)(5,6)(0,2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,-2)(-5,6) | 32 / 3678 |


| OV | AA (leads to GB) | QJ KG RL UX | EH AO CS MV | 5 | (0,0)(-4,6)(0,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(0,2)(4,6) | 48 / 3678 |


| OT | AH (leads to FA) | UJ LR VK MG | EH AP SW NC | 5 | (0,0)(5,4)(0,2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,-2)(-5,-4) | 32 / 3678 |


| OU | AC (leads to EA) | NJ LT KG MS | UH OA CQ EW | 5 | (0,0)(5,-4)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4)(-5,4) | 32 / 3678 |


| OW | AB (leads to JB) | JG LP KM SV | CQ HW AE NT | 5 | (0,0)(-3,2)(-2,0)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,0)(3,-2) | 16 / 3678 |


| AD (leads to 4) | HL NR IM OG | SW AE UJ CP | 5 | (0,0)(1,0)(4,4)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(-4,-4)(-1,0) | 16 / 3678 | |


| PV | AH (leads to GB) | RK LH GM SV | CI WP AE NT | 5 | (0,0)(-5,-4)(0,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(0,2)(5,4) | 72 / 3678 |


| PT | AF (leads to KB) | GP KM HL UX | SN QE AI CV | 5 | (0,0)(0,-2)(-4,0)(-1,0)(-3,0) | (0,0)(3,0)(1,0)(4,0)(0,2) | 48 / 3678 |


| PU | AC (leads to FA) | SK MG TL NH | CI WQ EU OA | 5 | (0,0)(4,6)(0,2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,-2)(-4,6) | 48 / 3678 |


| PS | AH (leads to GB) | RK LH GM UX | EI AP CS NV | 5 | (0,0)(-5,6)(0,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(0,2)(5,6) | 72 / 3678 |


| PQ | FD (leads to IA) | RL ND MK OC | EW GS UI AP | 5 | (0,0)(1,0)(3,-2)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,2)(-1,0) | 48 / 3678 |


| RQ | HA (leads to AH) | XF TK AS UL | MQ DI OB GV | 5 | (0,0)(0,1)(0,-2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,2)(0,-1) | 32 / 3678 |


| TQ | HA (leads to AH) | XF TI AS UJ | KO DG MB QV | 5 | (0,0)(2,1)(0,-2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,2)(-2,-1) | 32 / 3678 |


| QU | AD (leads to HC) | RS HM GI XL | PN TC EV AJ | 5 | (0,0)(3,0)(-4,-3)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(4,3)(-3,0) | 32 / 3678 |


| QS | AG (leads to GB) | GL MI HN SV | CJ WQ AE OT | 5 | (0,0)(6,-4)(0,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(0,2)(6,4) | 48 / 3678 |


| QW | AA (leads to JB) | RO HL GI UX | EM PA CS JV | 5 | (0,0)(1,0)(-2,0)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,0)(-1,0) | 16 / 3678 |


| 0 | GA (leads to NN) | KA CI LB DJ | SW OG UM QE | 4 | (0,0)(2,4)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(-2,-4) | 16 / 3678 |


| 2 | HA (leads to OQ) | AF KC BL GJ | WD SO UQ MH | 4 | (0,0)(-4,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(4,2) | 16 / 3678 |


| 4 | BA (leads to NN) | IA CG JB DH | SW MQ UK OE | 4 | (0,0)(4,4)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(-4,-4) | 10 / 3678 |


| DA | HA (leads to NN) | KW AI LX BJ | EU OG SM QC | 4 | (0,0)(2,6)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(-2,6) | 72 / 3678 |

| EA | DE (leads to TN) | GC EP DL FO | QA HU WJ MS | 4 | (0,0)(3,-4)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,4) | 72 / 3678 |


| EB | BB (leads to NT) | GV IS HJ CF | QT WM OA KD | 4 | (0,0)(-2,6)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,6) | 48 / 3678 |


| FA | EF (leads to NN) | MC EK ND FL | UA QI WO GS | 4 | (0,0)(0,2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,-2) | 96 / 3678 |


| FC | BA (leads to NT) | GS ID HJ XC | QE TM OV KA | 4 | (0,0)(-2,-3)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,3) | 32 / 3678 |


| GB | CD (leads to OQ) | AF GC BH OR | WD SK UM IP | 4 | (0,0)(0,-2)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(0,2) | 48 / 3678 |


| AH | AH (leads to NN) | MS UK NT VL | AE QI CO GW | 4 | (0,0)(0,-2)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2)(0,2) | 96 / 3678 |

| HC | GA (leads to NT) | IS KD JL XC | GE TO QV MA | 4 | (0,0)(-4,-3)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(4,3) | 32 / 3678 |


| IA | DE (leads to NT) | GA CP BL DO | QW HS UJ ME | 4 | (0,0)(3,-2)(2,1)(0,3) | (0,0)(0,-3)(-2,-1)(-3,2) | 72 / 3678 |

| IB | GA (leads to NT) | ID KA JL UX | GB EO QS MV | 4 | (0,0)(-4,0)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(4,0) | 48 / 3678 |


| JA | IA (leads to OQ) | WD KA XL GJ | UB EO SQ MH | 4 | (0,0)(-4,0)(-1,4)(-3,0) | (0,0)(3,0)(1,-4)(4,0) | 96 / 3678 |


| JB | BA (leads to NT) | GD IA HJ UX | QB EM OS KV | 4 | (0,0)(-2,0)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(2,0) | 64 / 3678 |


| KB | IB (leads to PW) | GD KA HL SV | QB EO WI MT | 4 | (0,0)(-4,0)(-1,0)(-3,0) | (0,0)(3,0)(1,0)(4,0) | 48 / 3678 |


| LB | AA (leads to PW) | GC KX HL FU | QA DO VI MS | 4 | (0,0)(-4,1)(-1,0)(-3,0) | (0,0)(3,0)(1,0)(4,-1) | 48 / 3678 |


| MA | BF (leads to PP) | MA EI NB FJ | UW QG KO CS | 4 | (0,0)(0,2)(3,2)(-3,-3) | (0,0)(3,3)(-3,-2)(0,-2) | 24 / 3678 |


| NU | GB (leads to PP) | OU AK PV BL | ES GI MQ WC | 4 | (0,0)(-2,6)(3,2)(-3,-3) | (0,0)(3,3)(-3,-2)(2,6) | 48 / 3678 |


| OS | CF (leads to PW) | OC GX PH FU | MA DK VQ IS | 4 | (0,0)(0,1)(-1,0)(-3,0) | (0,0)(3,0)(1,0)(0,-1) | 48 / 3678 |


| PR | FG (leads to NT) | KS MD LN XC | IE TQ GV OA | 4 | (0,0)(6,-3)(-1,-2)(-3,0) | (0,0)(3,0)(1,2)(6,3) | 48 / 3678 |


| QV | FB (leads to PW) | KD OA LP SV | IB EG WM QT | 4 | (0,0)(4,0)(-1,0)(-3,0) | (0,0)(3,0)(1,0)(-4,0) | 48 / 3678 |


| NN | GC (leads to UU) | AQ SK BR TL | WO EI MC GU | 3 | (0,0)(1,2)(-3,-3) | (0,0)(3,3)(-1,-2) | 36 / 3678 |


| NT | CF (leads to SV) | EP GM FH UX | CN QK AS IV | 3 | (0,0)(-1,-2)(-3,0) | (0,0)(3,0)(1,2) | 48 / 3678 |


| OQ | CF (leads to SV) | WP GM XH CF | UN QK SA ID | 3 | (0,0)(-1,4)(-3,0) | (0,0)(3,0)(1,-4) | 32 / 3678 |


| PP | GC (leads to UU) | AO SI BP TJ | WM EG KC QU | 3 | (0,0)(3,2)(-3,-3) | (0,0)(3,3)(-3,-2) | 36 / 3678 |


| PW | CB (leads to SV) | CP GM DH SV | AN QK WE IT | 3 | (0,0)(-1,0)(-3,0) | (0,0)(3,0)(1,0) | 24 / 3678 |


| RR | GC (leads to UU) | AR SL BG TM | WP EJ NC HU | 3 | (0,0)(0,2)(-3,-3) | (0,0)(3,3)(0,-2) | 16 / 3678 |


| RW | DA (leads to SV) | EO RL FG UX | CM PJ AS HV | 3 | (0,0)(0,-2)(-3,0) | (0,0)(3,0)(0,2) | 16 / 3678 |


| TU | FD (leads to SV) | IX LR AD MS | GV JP TB EN | 3 | (0,0)(3,0)(0,3) | (0,0)(0,-3)(-3,0) | 32 / 3678 |


| SV | DB (leads to TT) | OC FL PG SV | MA DJ WQ HT | 2 | (0,0)(-3,0) | (0,0)(3,0) | 72 / 3678 |


| UU | DB (leads to TT) | OF UL PG VA | MD SJ BQ HW | 2 | (0,0)(-3,-3) | (0,0)(3,3) | 16 / 3678 |


| TT | FB (leads to WW) | LO RI AD SV | JM PG WB ET | 1 | (0,0) | (0,0) | 16 / 3678 |


| WW | none | none | none | 0 | none | none | 4 / 3678 |
Author: Mike Hughey
Created: 07 September 2010
Last updated: 12 October 2010